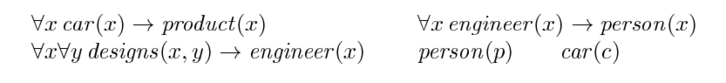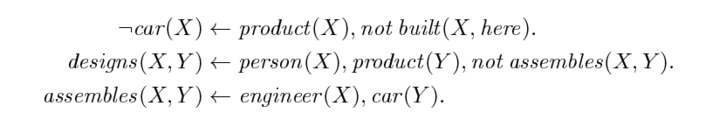TUWIEN Paraconsistent Hybrid Theories
From ONTORULE Show Case
Overview
This component provides a paraconsistent semantics for hybrid theories.
A hybrid theory is a theory over a language that is split into two parts, a part that is designated as classical, also called structural part, and a so-called program part, interpretated under nonmonotonic answer-set semantics.
For instance, hybrid knowledge bases are a tight coupling of ontologies and logical rules and constitute special (syntactically restricted) cases of hybrid theories.
Paraconsistent reasoning allows to draw non-trivial conclusions from an inconstant theory. Thus, it may serve the purpose of analyzing an inconsistent theory, as well as to maintain operability, i.e., still provide meaningful answers, when the underlying theory is inconsistent.
Example
Consider the following hybrid theory, consisting of a structural part representing information about cars and persons designing and engineering them:
And a rules part, additionally taking into account information on car assembly:
While both parts taken individually are consistent pieces of knowledge (the rules part also if the knowledge about the concrete instances is taken into account, i.e., that c is a car, and p a person), their combination is both inconsistent (wrt. c being a car or not) and incoherent (wrt. p assembling c, or not). However, this hybrid theory does have paraconsistent models, that allow for non-trivial conclusions, for instance that designs(p,c) holds.
Technical Work
Work carried out within the ONTORULE project extended previous work on paraconsistent reasoning for classical theories and Description Logics, as well as work on paraconsistent and paracoherent answer-set semantics for logic programs. Generalizing previous approaches, we developed a novel semantics for paraconsistent reasoning from hybrid theories, that however coincides with the standard semantics in case the combination is consistent.
The semantics is founded on an underlying nine-valued logic which has been rigorously developed and studied. We also investigated semantic properties of the resulting semantics, which establish that corresponding design objectives in terms of desirable properties have been met. An analysis of the computational complexity for major reasoning tasks in practically relevant fragments of the language complements our achievements concerning paraconsistent hybrid theories.
Corresponding results are reported in Deliverable 2.6.
| Belongs To Work Flow Step | Management +, and Execution + |
| Component Description | a semantics for hybrid theories that allows to draw non-trivial conclusions in case of inconsistency |
| Component Name | TUWIEN Paraconsistent Reasoning for Hybrid Theories + |
| Creation dateThis property is a special property in this wiki. | 25 November 2011 13:55:45 + |
| CreatorThis property is a special property in this wiki. | Michael.fink + |
| Implementing Vendor | Technische Universität Wien + |
| Last modified byThis property is a special property in this wiki. | Roman.korf + |